Lattices and Geometry#

This page contains documentation about Lattices and Geometry classes of qlbm. Lattices and geometry go hand-in-hand in that they do not themselves contain quantum components, but instead provide a convenient interface for accessing the information that determines the structure and composition of quantum components.

Lattices#

Lattices are the backbone of qlbm quantum components. While they do not contain quantum circuits themselves, lattices encode the information that makes implementing and extending QLBM quantum circuits seamless. Concretely, each Lattice fulfills the following functionality:

Infers the number of qubits required to construct a quantum circuit based on a user specification.
Warn the user of invalid or ill-formed specifications.
Group the qubits into separate quantum registers according to their functionality.
Provide convenient indexing methods methods to access individual (or groups of) qubits based on their purpose.
Encode additional information required for the automatic assembly of large quantum circuits.

class qlbm.lattice.lattices.collisionless_lattice.CollisionlessLattice(lattice_data, logger=<Logger qlbm (WARNING)>)[source]#

Implementation of the Lattice base specific to the 2D and 3D CQLBM algorithm developed by Schalkers and Möller [5].

Attribute	Summary
`num_dims`	The number of dimensions of the lattice.
`num_gridpoints`	A `List[int]` of the number of gridpoints of the lattice in each dimension. Important: for easier compatibility with binary arithmetic, the number of gridpoints specified in the input dictionary is one larger than the one held in the `Lattice`. That is, for a `16x64` lattice, the `num_gridpoints` attribute will have the value `[15, 63]`.
`num_grid_qubits`	The total number of qubits required to encode the lattice grid.
`num_velocity_qubits`	The total number of qubits required to encode the velocity discretization of the lattice.
`num_ancilla_qubits`	The total number of ancilla (non-velocity, non-grid) qubits required for the quantum circuit to simulate this lattice.
`num_total_qubits`	The total number of qubits required for the quantum circuit to simulate the lattice. This is the sum of the number of grid, velocity, and ancilla qubits.
`registers`	A `Tuple[qiskit.QuantumRegister, ...]` that holds registers responsible for specific operations of the QLBM algorithm.
`circuit`	An empty `qiskit.QuantumCircuit` with labeled registers that quantum components use as a base. Each quantum component that is parameterized by a `Lattice` makes a copy of this quantum circuit to which it appends its designated logic.
`shapes`	A `Dict[str, List[Shape]]` that contains all of the `Shape`s encoding the solid geometry of the lattice. The key of the dictionary is the specific kind of boundary condition of the obstacle (i.e., `"bounceback"` or `"specular"`).
`logger`	The performance logger, by default `getLogger("qlbm")`.

The registers encoded in the lattice and their accessors are given below. For the size of each register, \(N_{g_j}\) is the number of grid points of dimension \(j\) (i.e., 64, 128), \(N_{v_j}\) is the number of discrete velocities of dimension \(j\) (i.e., 2, 4), and \(d\) is the total number of dimensions: 2 or 3.

Register allocation#
Register	Size	Access Method	Description
`ancilla_velocity_register`	\(d\)	`ancillae_velocity_index()`	The qubits controlling the streaming operation based on the CFL counter.
`ancilla_obstacle_register`	\(d\) or \(1\), See Adaptable Lattice Register.	`ancillae_obstacle_index()`	The qubits used to detect whether particles have streamed into obstacles. Used for reflection.
`ancilla_comparator_register`	\(2(d-1)\)	`ancillae_comparator_index()`	The qubits used to for `Comparator`s. Used for reflection.
`grid_registers`	\(\Sigma_{1\leq j \leq d} \left \lceil{\log N_{g_j}} \right \rceil\)	`grid_index()`	The qubits encoding the physical grid.
`velocity_registers`	\(\Sigma_{1\leq j \leq d} \left \lceil{\log N_{v_j}} \right \rceil - 1\)	`velocity_index()`	The qubits encoding speeds.
`velocity_dir_registers`	\(d\)	`velocity_dir_index()`	The qubits encoding velocity direction (positive or negative).

Adaptable Lattice Register#

The BounceBackReflectionOperator and SpecularReflectionOperator have different requirements for the number of qubits. If a lattice contains at least one SR-conditioned object, then \(d\) ancilla qubits are required to flag whether the particle has collided with the surface of the object, its edge (in 3D), or its corner. This information influences which directional qubits are inverted.

The BB boundary conditions are simpler in that they only require \(1\) ancilla qubit to detect whether a particle has collided with the object. All velocities are inverted, irrespective of the interaction with the object. As such, if only the lattice only contains BB objects, a single ancilla qubit is required for reflection across all objects. The lattice object infers this at construction time and adjusts the relative index of all other registers accordingly.

A lattice can be constructed from from either an input file or a Python dictionary. A sample configuration might look as follows:

{
    "lattice": {
        "dim": {
            "x": 16,
            "y": 16
        },
        "velocities": {
            "x": 4,
            "y": 4
        }
    },
    "geometry": [
        {
            "x": [9, 12],
            "y": [3, 6],
            "boundary": "specular"
        },
        {
            "x": [9, 12],
            "y": [9, 12],
            "boundary": "bounceback"
        }
    ]
}

The register setup can be visualized by constructing a lattice object:

from qlbm.lattice import CollisionlessLattice

CollisionlessLattice(
    {
        "lattice": {"dim": {"x": 8, "y": 8}, "velocities": {"x": 4, "y": 4}},
        "geometry": [{"shape":"cuboid", "x": [5, 6], "y": [1, 2], "boundary": "bounceback"}],
    }
).circuit.draw("mpl")

(Source code, png, hires.png, pdf)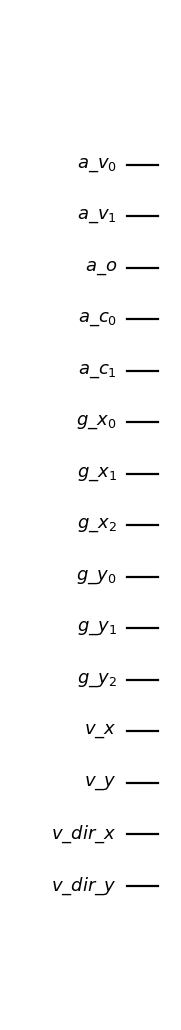

logger: Logger#: The performance logger, by default getLogger("qlbm").

num_dims: int#: The number of dimensions of the system.

num_gridpoints: List[int]#: The number of gridpoints of the lattice in each dimension.

Warning

For easier compatibility with binary arithmetic, the number of gridpoints specified in the input dictionary is one larger than the one held in the Lattice s. That is, for a \(16 \times 64\) lattice, the num_gridpoints attribute will have the value [15, 63].

num_velocities: List[int]#: The number of velocities in each dimension. This will be refactored in the future to support \(D_dQ_q\) discretizations.

Warning

For easier compatibility with binary arithmetic, the number of velocities specified in the input dictionary is one larger than the one held in the Lattice s. If the numbers of discrete velocities are \(4\) and \(2\), the num_velocities attribute will have the value [3, 1].

num_total_qubits: int#: The total number of qubits required for the quantum circuit to simulate the lattice. This is the sum of the number of grid, velocity, and ancilla qubits.

ancillae_velocity_index(dim=None)[source]#

Get the indices of the qubits used as velocity ancillae for the specified dimension.

Parameters:: dim (int | None, optional) – The dimension of the grid for which to retrieve the velocity qubit indices, by default None. When dim is None, the indices of ancillae qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used as velocity ancillae for the given dimension.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

ancillae_obstacle_index(index=None)[source]#

Get the indices of the qubits used as obstacle ancilla for the specified dimension.

Parameters:: index (int | None, optional) – The index of the grid for which to retrieve the obstacle qubit index, by default None. When index is None, the indices of ancillae qubits for all dimensions are returned. For 2D lattices with only bounce-back boundary-conditions, only one obstacle qubit is required. For all other configurations, the algorithm uses 2d-2 obstacle qubits.
Returns:: A list of indices of the qubits used as obstacle ancilla for the given dimension.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

ancillae_comparator_index(index=None)[source]#

Get the indices of the qubits used as comparator ancillae for the specified index.

Parameters:: index (int | None, optional) – The index for which to retrieve the comparator qubit indices, by default None. There are num_dims-1 available indices (i.e., 1 for 2D and 2 for 3D). When index is None, the indices of ancillae qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used as obstacle ancilla for the given dimension. By convention, the 0th qubit in the returned list is used for lower bound comparison and the 1st is used for upper bound comparisons.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

grid_index(dim=None)[source]#

Get the indices of the qubits used that encode the grid values for the specified dimension.

Parameters:: dim (int | None, optional) – The dimension of the grid for which to retrieve the grid qubit indices, by default None. When dim is None, the indices of all grid qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used to encode the grid values for the given dimension.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

velocity_index(dim=None)[source]#

Get the indices of the qubits used that encode the velocity magnitude values for the specified dimension.

Parameters:: dim (int | None, optional) – The dimension of the grid for which to retrieve the velocity qubit indices, by default None. When dim is None, the indices of all velocity magnitude qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used to encode the velocity magnitude values for the given dimension.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

velocity_dir_index(dim=None)[source]#

Get the indices of the qubit that encodes the velocity direction values for the specified dimension.

Parameters:: dim (int | None, optional) – The dimension of the grid for which to retrieve the velocity direction qubit index, by default None. When dim is None, the indices of all velocity direction qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used to encode the velocity direction for the given dimension.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

get_registers()[source]#

Generates the encoding-specific register required for the streaming step.

For this encoding, different registers encode (i) the velocity direction, (ii) the velocity discretization, (iii) the velocity ancillae, and (iv) the grid encoding.

Returns:: Tuple[QuantumRegister]: The 4-tuple of qubit registers encoding the streaming step.
Return type:: List[int]

logger_name()[source]#

An identifiable name to be used in the logger to help with benchmarking and analysis.

Returns:: A string that can be used to sufficiently identify the lattice specification.
Return type:: str

has_multiple_geometries()[source]#

Whether multiple lattice geometries are simulated simultaneously.

Returns:: Whether multiple lattice geometries are simulated simultaneously.
Return type:: bool

Parameters:

lattice_data (str | Dict)
logger (Logger)

class qlbm.lattice.lattices.spacetime_lattice.SpaceTimeLattice(num_timesteps, lattice_data, filter_inside_blocks=True, include_measurement_qubit=False, use_volumetric_ops=False, logger=<Logger qlbm (WARNING)>)[source]#

Implementation of the Lattice base specific to the 2D and 3D SpaceTimeQLBM algorithm developed by Schalkers and Möller [7].

Warning

The STQBLM algorithm is a based on typical \(D_dQ_q\) discretizations. The current implementation only supports \(D_2Q_4\) for one time step. This is work in progress. Multiple steps are possible through qlbm‘s reinitialization mechanism.

Attribute	Summary
`num_timesteps`	The number of time steps the lattice should be simulated for.
`num_dims`	The number of dimensions of the lattice.
`num_gridpoints`	A `List[int]` of the number of gridpoints of the lattice in each dimension. Important: for easier compatibility with binary arithmetic, the number of gridpoints specified in the input dictionary is one larger than the one held in the `Lattice`. That is, for a `16x64` lattice, the `num_gridpoints` attribute will have the value `[15, 63]`.
`num_grid_qubits`	The total number of qubits required to encode the lattice grid.
`num_velocity_qubits`	The total number of qubits required to encode the velocity discretization of the lattice.
`num_ancilla_qubits`	The total number of ancilla (non-velocity, non-grid) qubits required for the quantum circuit to simulate this lattice. There are no ancilla qubits for the Space-Time QLBM.
`num_total_qubits`	The total number of qubits required for the quantum circuit to simulate the lattice. This is the sum of the number of grid, velocity, and ancilla qubits.
`registers`	A `Tuple[qiskit.QuantumRegister, ...]` that holds registers responsible for specific operations of the QLBM algorithm.
`circuit`	An empty `qiskit.QuantumCircuit` with labeled registers that quantum components use as a base. Each quantum component that is parameterized by a `Lattice` makes a copy of this quantum circuit to which it appends its designated logic.
`blocks`	A `Dict[str, List[Block]]` that contains all of the `Block`s encoding the solid geometry of the lattice. The key of the dictionary is the specific kind of boundary condition of the obstacle (i.e., `"bounceback"` or `"specular"`).
`logger`	The performance logger, by default `getLogger("qlbm")`.

The registers encoded in the lattice and their accessors are given below. For the size of each register, \(N_{g_j}\) is the number of grid points of dimension \(j\) (i.e., 64, 128), \(N_{v_j}\) is the number of discrete velocities of dimension \(j\) (i.e., 2, 4), and \(d\) is the total number of dimensions: 2 or 3.

Register allocation#
Register	Size	Access Method	Description
`grid_registers`	\(\Sigma_{1\leq j \leq d} \left \lceil{\log N_{g_j}} \right \rceil\)	`grid_index()`	The qubits encoding the physical grid.
`velocity_registers`	\(\min(N_g \cdot N_v, \frac{N_v^2\cdot N_t \cdot (N_t + 1)}{2} + N_v)\)	`velocity_index()`	The qubits encoding local and neighboring velocities.

A lattice can be constructed from from either an input file or a Python dictionary. Currently, only the \(D_2Q_4\) discretization is supported, and no boundary conditions are implemented. A sample configuration might look as follows. Keep in mind that the velocity and geometry section should not be altered in this current implementation.

{
    "lattice": {
        "dim": {
            "x": 16,
            "y": 16
        },
        "velocities": "D2Q4"
    },
    "geometry": []
}

The register setup can be visualized by constructing a lattice object:

from qlbm.lattice import SpaceTimeLattice

SpaceTimeLattice(
    num_timesteps=1,
    lattice_data={
        "lattice": {"dim": {"x": 4, "y": 8}, "velocities": "D2Q4"},
        "geometry": [],
    }
).circuit.draw("mpl")

(Source code, png, hires.png, pdf)

Parameters:

num_timesteps (int)
lattice_data (str | Dict)
filter_inside_blocks (bool)
include_measurement_qubit (bool)
use_volumetric_ops (bool)
logger (Logger)

grid_index(dim=None)[source]#

Get the indices of the qubits used that encode the grid values for the specified dimension.

Parameters:: dim (int | None, optional) – The dimension of the grid for which to retrieve the grid qubit indices, by default None. When dim is None, the indices of all grid qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used to encode the grid values for the given dimension.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist.

velocity_index(point_neighborhood_index, velocity_direction=None)[source]#

Get the indices of the qubits used that encode the velocity for a specific neighboring grid point and direction.

Parameters:

point_neighborhood_index (int) – The index of the grid point neighbor.
velocity_direction (int | None, optional) – The index of the discrete velocity according to the LBM discretization, by default None. When velocity_direction is None, the indices of all velocity qubits of the neighbor are returned.

Returns:

A list of indices of the qubits that encode the specific neighbor, velocity pair.

Return type:

List[int]

ancilla_mass_index()[source]#

Get the index of the qubit used as the mass measurement ancilla.

Returns:: The index of the mass measurement qubit.
Return type:: List[int]
Raises:: LatticeException – If the mass measurement qubit is toggled off.

ancilla_comparator_index(index=None)[source]#

Get the indices of the qubits used as comparator ancillae for the specified index.

Parameters:: index (int | None, optional) – The index for which to retrieve the comparator qubit indices, by default None. There are num_dims-1 available indices (i.e., 1 for 2D and 2 for 3D). When index is None, the indices of ancillae qubits for all dimensions are returned.
Returns:: A list of indices of the qubits used as obstacle ancilla for the given dimension. By convention, the 0th qubit in the returned list is used for lower bound comparison and the 1st is used for upper bound comparisons.
Return type:: List[int]
Raises:: LatticeException – If the dimension does not exist or if the lattice is set up such that it contains no ancilla qubits for volumetric operations.

volumetric_ancilla_qubit_combinations(overflow_occurred)[source]#

Get all combinations of ancilla qubit indices required for volumetric operations.

Volumetric operations perform actions on contiguous volumes of space in the lattice. These volumes are defined by lower and upper bounds in each dimension. Since the locality of the data structure may be affected by periodic boundary conditions, volumetrics must be adjusted to account for all possible overflow scenarios. This is done by performing the operations in different orders on the adjusted bounds. This method returns the sequence of ancilla qubit indices required to perform the operations soundly.

Parameters:: overflow_occurred (List[bool]) – A \(d\)-length list of booleans indicating whether overflow occurred in each dimension.
Returns:: The sequence of ancilla qubit indices required to perform the volumetric operations.
Return type:: List[List[int]]
Raises:: LatticeException – If volumetric operations are not enabled in the lattice.

get_registers()[source]#

Generates the registers on which the quantum circuits will be placed.

Returns:: A fixed number of registers according to the lattice specification.
Return type:: Tuple[List[QuantumRegister], …]

is_inside_an_obstacle(gridpoint)[source]#

Whether a gridpoint is inside the volume of any obstacle in the lattice.

Parameters:: gridpoint (Tuple[int, ...]) – The \(d\)-dimensional gridpoint to check.
Returns:: Whether the gridpoint is inside any obstacle.
Return type:: bool

logger_name()[source]#

An identifiable name to be used in the logger to help with benchmarking and analysis.

Returns:: A string that can be used to sufficiently identify the lattice specification.
Return type:: str

comparator_periodic_volume_bounds(bounds)[source]#

Computes the lower and upper bounds for the Comparators used to perform volumetric operations in the SpaceTimeQLBM.

For any given lower and upper bounds in 1, 2, or 3 dimensions, modulo operations are applied that detect whether periodic boundary conditions are required. If that is the case, the directions in which the bounds overflow becomes the opposite kind of bound. For instance, a \(-2 \leq x \leq 7\) interval that would require a \(-2 \leq x \leq 7\) on a \(16 \\times 16\) would require a \(\geq 2\) comparator and a \(\leq 7\) comparator. Since \(-2\) is not part of the domain, it gets mapped to \(14\), and a different operation, based on two \(\geq\) comparators is required.

Parameters:: bounds (List[Tuple[int, int]]) – The absolute bounds of the volume in each dimensions.
Returns:: The bounds adjusted for periodicity and whether overflow occurs for each bound.
Return type:: List[Tuple[Tuple[int, int], Tuple[bool, bool]]]

has_multiple_geometries()[source]#

Whether multiple lattice geometries are simulated simultaneously.

Returns:: Whether multiple lattice geometries are simulated simultaneously.
Return type:: bool

Geometry#

Processing obstacle geometry into quantum circuits is a tedious and error-prone task when performed manually. To alleviate this challenge, qlbm provides Block and Circle classes that parse the geometry information supplied as part of the Lattice specification into information that parameterized the construction of quantum circuits. This includes the position of the obstacle within the grid and its boundary conditions. In addition, these shapes contain triangulation methods that allow them to be exported as stl files and visualized in Paraview.

Each shape contains snippets of information that determine how individual components of reflection behave. To make the generation of this circuits more manageable, we segment the block information into different categories of edge cases, which are also broken down by algorithm.

The CQLBM algorithm uses the following data structures:

DimensionalReflectionData models the isolated, one-dimensional features of a fixed point on the grid.
ReflectionPoint models the 2D or 3D information of a fixed point in space.
ReflectionWall models the 2D or 3D information of the wall of the obstacle.
ReflectionResetEdge models the 3D information of an edge along the walls of an obstacle.

The SpaceTimeQLBM algorithm on makes use of the following:

SpaceTimePWReflectionData models the reflection data of a single grid point of the lattice.
SpaceTimeVolumetricReflectionData models the reflection data of a contiguous volume in space.
SpaceTimeDiagonalReflectionData of diagonals in 2D.

Note

CQLBM and SpaceTimeQLBM support different kinds of geometry. For CQLBM, geometry objects can only be 2D or 3D cuboids, and they must be placed at least two grid points apart for consistent behavior. SpaceTimeQLBM supports 2D rectangles of arbitrary lengths, as well as circles.

class qlbm.lattice.geometry.Block(bounds, num_grid_qubits, boundary_condition, num_gridpoints=None)[source]#

Contains information required for the generation of boundary conditions for an axis-parallel cuboid obstacle.

Available for the specular reflection and bounce-back for the CQLBM algorithm and bounce-back for the STQBM algorithm. A block can be constructed from minimal information, see the Table below.

Constructor parameters#
Parameter	Description
`bounds`	A `List[Tuple[int, int]]` of lower and upper bounds in each dimension. For example, `[(2, 5), (10, 12)]`; `[(2, 5), (9, 12), (33, 70)]`.
`num_qubits`	The number of grid qubits of the underlying lattice.
`boundary_condition`	A string indicating the type of boundary condition of the block. Should be either `"specular"` or `"bounceback"`.

The Block constructor will parse this information and automatically infer all of the information required to perform all of the reflection edge cases. This data is split over several attributes, see the table below.

Class attributes#
Attribute	Description
`bounds`	The `List[Tuple[int, int]]` of lower and upper bounds in each dimension. For example, `[(2, 5), (10, 12)]`; `[(2, 5), (9, 12), (33, 70)]`.
`inside_points_data`	The `List[Tuple[DimensionalReflectionData, ...]]` data encoding the corner points on the inside of the obstacle. The outer list contains \(d\) entries, one per dimension. Each entry is a tuple of `DimensionalReflectionData` of the lower and upper bounds of that dimension, respectively.
`outside_points_data`	The `List[Tuple[DimensionalReflectionData, ...]]` data encoding the corner points on the outside of the obstacle. The outer list contains \(d\) entries, one per dimension. Each entry is a tuple of `DimensionalReflectionData` of the lower and upper bounds of that dimension, respectively.
`walls_inside`	The `List[List[ReflectionWall, ...]]` data encoding the walls of the inside of the obstacle. The outer list contains \(d\) entries, one per dimension. Each inner list is a list of two `ReflectionWall`s of the lower and upper bounds of that dimension, respectively.
`walls_outside`	The `List[List[ReflectionWall, ...]]` data encoding the walls of the outside of the obstacle. The outer list contains \(d\) entries, one per dimension. Each inner list is a list of two `ReflectionWall`s of the lower and upper bounds of that dimension, respectively.
`corners_inside`	The `List[ReflectionPoint]` data encoding the corner points on the inside of the obstacle. There are 4 inner corner `ReflectionPoint`s per obstacle in 2D, and 8 in 3D.
`corners_outside`	The `List[ReflectionPoint]` data encoding the corner points on the outside of the obstacle. There are 4 outer corner `ReflectionPoint`s per obstacle in 2D, and 8 in 3D.
`near_corner_points_2d`	The `List[ReflectionPoint]` data encoding points on the outside of the object that are adjacent to inner corner points. These points require additional logic in the quantum circuit for particles that have streamed without reflecting off the obstacle. Only applicable to 2D example, since 3D example use edges instead. There are 8 near-corner `ReflectionPoint` s per obstacle.
`corner_edges_3d`	The `List[ReflectionResetEdge]` data encoding edges on the outside of the object that are adjacent to corners of the obstacle. Used to reset ancilla qubit states after reflection. There are 12 corner `ReflectionResetEdge` s per obstacle.
`near_corner_edges_3d`	The `List[ReflectionResetEdge]` data encoding edges on the outside of the object that are adjacent either side of `corner_edges_3d`. These edges require additional logic in the quantum circuit for particles that have streamed without reflecting off the obstacle. There are 24 near-corner `ReflectionResetEdge` s per obstacle.
`overlapping_near_corner_edge_points_3d`	The `List[ReflectionPoint]` data encoding the set of points at the intersections of `near_corner_edges_3d`. These points require additional logic in to account for the fact that the state of obstacle ancilla qubits was doubly reset (once by each edge). There are 24 such `ReflectionPoint` s per obstacle.

Parameters:

bounds (List[Tuple[int, int]])
num_grid_qubits (List[int])
boundary_condition (str)
num_gridpoints (List[int] | None)

get_spacetime_reflection_data_d1q2(properties, num_steps=None)[source]#

Calculate space-time reflection data for \(D_1Q_2\) SpaceTimeQLBM lattice.

Parameters:

properties (SpaceTimeLatticeBuilder) – The lattice discretization properties.
None (num_steps int |) – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.
optional – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.
num_steps (int | None)

Returns:

The information encoding the reflections to be performed.

Return type:

List[SpaceTimeReflectionData]

get_spacetime_reflection_data_d2q4(properties, num_steps=None)[source]#

Calculate space-time reflection data for \(D_2Q_4\) SpaceTimeQLBM lattice.

Parameters:

properties (SpaceTimeLatticeBuilder) – The lattice discretization properties.
num_steps (int | None, optional) – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.

Returns:

The information encoding the reflections to be performed.

Return type:

List[SpaceTimeReflectionData]

get_d2q4_volumetric_reflection_data(properties, num_steps=None)[source]#

Calculate volumetric reflection data for \(D_2Q_4\) SpaceTimeQLBM lattice.

Parameters:

properties (SpaceTimeLatticeBuilder) – The lattice discretization properties.
None (num_steps int |) – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.
optional – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.
num_steps (int | None)

Returns:

The information encoding the reflections to be performed.

Return type:

List[SpaceTimeVolumetricReflectionData]

get_d2q4_surfaces()[source]#

Get all surfaces of the block in 2 dimensions.

The information is formatted as List[List[List[Tuple[int, ...]]]]. The outermost list is by dimension. The middle list contains two lists pertaining to the lower and upper bounds of the block in that dimenison. The innermost list contains the gridpoints that make up the surface encoded as tuples.

Returns:: The block surfaces in two dimensions.
Return type:: List[List[List[Tuple[int, …]]]]

get_lqlga_reflection_data_d1q2()[source]#: Calculate space-time reflection data for \(D_1Q_2\) LQLGA.

get_lqlga_reflection_data_d1q3()[source]#: Calculate space-time reflection data for \(D_1Q_3\) LQLGA.

contains_gridpoint(gridpoint)[source]#

Whether the block contains a given gridpoint within its volume.

Parameters:: gridpoint (Tuple[int, ...]) – The gridpoint to check for.
Returns:: Whether the gridpoint is within the block.
Return type:: bool

stl_mesh()[source]#

Provides the stl representation of the shape.

Returns:: The mesh representing the shape.
Return type:: stl.mesh.Mesh

to_json()[source]#

Serializes the shape to JSON format.

Returns:: The JSON representation of the shape.
Return type:: str

name()[source]#

The name of the shape.

Returns:: The name of the shape.
Return type:: str

to_dict()[source]#

Produces a dictionary representation of the shape.

Returns:: A dictionary representation of the bounds and boundary conditions of the shape.
Return type:: Dict[str, List[int] | str]

class qlbm.lattice.geometry.Circle(center, radius, num_grid_qubits, boundary_condition, num_mesh_segments=50)[source]#

Contains information required for the generation of bounce-back boundary conditions for the STQBM algorithm.

A circle can be constructed from minimal information, see the Table below.

Constructor parameters#
Parameter	Description
`center`	A `Tuple[int, ...]` specifying the center of the circle. For example, `(2, 5)`.
`radius`	An `int` specifying the radius of the circle. For example, `3`.
`num_grid_qubits`	The number of grid qubits of the underlying lattice.
`boundary_condition`	A `string` indicating the type of boundary condition of the block. At the moment, only `"bounceback"` is supported.
`num_mesh_segments`	An `int` that describes how fine the `stl` of the object is.

The Circle constructor will parse this information and automatically infer all of the information required to perform all of the reflection edge cases. Class attributes are described in the table below.

Class attributes#
Attribute	Description
`perimeter_points`	The `List[Tuple[int, int]]` of all gridpoints that lie on the perimeter of the circle, and are therefore relevant for boundary conditions.

Parameters:

center (Tuple[int, ...])
radius (int)
num_grid_qubits (List[int])
boundary_condition (str)
num_mesh_segments (int)

get_circle_perimeter()[source]#

Uses Bresenham’s circle drawing algorithm to specify all points along the perimeter of the circle.

Returns:: All gridpoints that lie on the perimeter of the circle
Return type:: List[Tuple[int, int]]

stl_mesh()[source]#

Provides the stl representation of the shape.

Returns:: The mesh representing the shape.
Return type:: stl.mesh.Mesh

is_point_on_segment(gridpoint, segment)[source]#

Whether the point belongs to a given axis-aligned segment.

Parameters:

gridpoint (Tuple[int, int]) – The gridpoint to test for.
segment (List[Tuple[int, int]]) – The segment to test for.

Returns:

Whether the point belongs to a given axis-aligned segment.

Return type:

bool

is_point_on_any_segment(gridpoint, segments)[source]#

Whether the point belongs to any axis-aligned segment in a given list.

Parameters:

gridpoint (Tuple[int, int]) – The gridpoint to test for.
segments (List[List[Tuple[int, int]]]) – The segments to test for.

Returns:

Whether the point lays on any of the given segments.

Return type:

bool

split_perimeter_points(points)[source]#

Splits point on the perimeter of the circle into three categories.

Points belong to either (1) axis-aligned segments (2) diagonal segments, or (3) individual points.

Axis-aligned and diagonal segments are encoded as the two ends of the segment. Individual points are simply listed by their coordinates. The results are returned in the order listed previously.

Parameters:: points (List[Tuple[int, int]]) – The gridpoints on the perimeter of the circle.
Returns:: The points classified by which category they belong to.
Return type:: Tuple[List[Tuple[int, int]], List[List[Tuple[int, int]]], List[Tuple[int, int]]]

to_json()[source]#

Serializes the shape to JSON format.

Returns:: The JSON representation of the shape.
Return type:: str

name()[source]#

The name of the shape.

Returns:: The name of the shape.
Return type:: str

to_dict()[source]#

Produces a dictionary representation of the shape.

Returns:: A dictionary representation of the bounds and boundary conditions of the shape.
Return type:: Dict[str, List[int] | str]

contains_gridpoint(gridpoint)[source]#

Whether the block contains a given gridpoint within its volume.

Parameters:: gridpoint (Tuple[int, ...]) – The gridpoint to check for.
Returns:: Whether the gridpoint is within the block.
Return type:: bool

get_spacetime_reflection_data_d1q2(properties, num_steps=None)[source]#

Calculate space-time reflection data for \(D_1Q_2\) SpaceTimeQLBM lattice.

Parameters:

properties (SpaceTimeLatticeBuilder) – The lattice discretization properties.
None (num_steps int |) – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.
optional – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.

Returns:

The information encoding the reflections to be performed.

Return type:

List[SpaceTimeReflectionData]

get_spacetime_reflection_data_d2q4(properties, num_steps=None)[source]#

Calculate space-time reflection data for \(D_2Q_4\) SpaceTimeQLBM lattice.

Parameters:

properties (SpaceTimeLatticeBuilder) – The lattice discretization properties.
num_steps (int | None, optional) – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.

Returns:

The information encoding the reflections to be performed.

Return type:

List[SpaceTimeReflectionData]

get_d2q4_volumetric_reflection_data(properties, num_steps=None)[source]#

Calculate volumetric reflection data for \(D_2Q_4\) SpaceTimeQLBM lattice.

Parameters:

properties (SpaceTimeLatticeBuilder) – The lattice discretization properties.
None (num_steps int |) – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.
optional – Number of timesteps to calculate reflections for. If None, uses properties.num_timesteps. Defaults to None.

Returns:

The information encoding the reflections to be performed.

Return type:

List[SpaceTimeVolumetricReflectionData]

static expand_axis_segments(axis_segments)[source]#

Expands axis-aligned segments encoded as the two extremes of the segment into lists of all points contained within each segment.

Parameters:: axis_segments (List[List[Tuple[int, int]]]) – The segments to expand.
Returns:: All points within each segment.
Return type:: List[Tuple[int, int]]

static expand_diagonal_segments(diagonal_segments)[source]#

Expands diagonal segments encoded as the two extremes of the segment into lists of all points contained within each segment.

Parameters:: diagonal_segments (List[List[Tuple[int, int]]]) – The diagonal segments to expand
Returns:: All points within each segment.
Return type:: List[Tuple[int, …]]

class qlbm.lattice.geometry.DimensionalReflectionData(qubits_to_invert, bound_type, is_outside_obstacle_bounds, gridpoint_encoded, dim, name)[source]#

Contains one-dimensional information about the position of a grid point relevant to the obstacle.

Used for edge cases relating to either inside or outside corner points.

Class attributes#
Attribute	Description
`qubits_to_invert`	The `List[int]` of qubit indices that should be inverted in order to convert the state of grid qubits encoding this dimension to \(\ket{1}^{\otimes n_{g_d}}\). See the example below.
`bound_type`	The `bool` indicating the type of bound this point belongs to. `False` indicates a lower bound, and `True` indicates an upper bound.
`is_outside_obstacle_bounds`	The `bool` indicating the whether the point belongs to the solid domain. `False` that the point is inside the solid domain, and `True` indicates the outside.
`dim`	The `int` indicating which dimension this object refers to.
`gridpoint_encoded`	The `int` indicating which grid point this object encodes. Used for debugging purposes.
`name`	A string assigned to each dimensional data object in the `Block` constructor. Used for debugging purposes.

Note

Consider for example encoding the grid point at location 2 (encoded as \(\ket{010}\)) on the \(x\)-axis on an \(8\\times 8\) 2D grid.

The DimensionalReflectionData object encoding this information would have a qubits_to_invert value of [0, 2]. This means that the \(0^{th}\) and \(2^{nd}\) qubits would have to be inverted to produce the \(\ket{111}\) state. This information is passed on to the reflection operators, which place the \(X\) gates at the appropriate positions in the register, and can then use the \(g_x\) register to control reflection.

If we wanted to encode point \(3\) (\(\ket{011}\)) on \(y\)-axis on the same grid, this would result in qubits_to_invert = [5], since the most significant qubit (index 2 of the \(y\)-axis) is encoded last in the register, and there are 3 qubits encoding the \(x\)-axis “in front” of it.

Parameters:

qubits_to_invert (List[int])
bound_type (bool)
is_outside_obstacle_bounds (bool)
gridpoint_encoded (int)
dim (int)
name (str)

class qlbm.lattice.geometry.ReflectionPoint(data, dims_inside, dims_outside, inversion_function)[source]#

Encodes the information required to perform reflection on a single point.

A point is encoded as 2 or 3 fixed DimensionalReflectionData objects, one per dimension. This classes processes the information encoded in the reflection data objects into boolean valued attributes that determine whether the directional velocity qubits should be inverted to perform reflection.

Class attributes#
Attribute	Description
`data`	The `List[DimensionalReflectionData]` containing the point data for each dimension.
`num_dims`	The `int` number of dimensions of this point (also of the corresponding lattice).
`dims_inside`	The `List[int]` that specifies which of the `data` entries are inside obstacle bounds in their respective dimension.
`dims_outside`	The `List[int]` that specifies which of the `data` entries are outside obstacle bounds in their respective dimension.
`qubits_to_invert`	The `List[int]` of qubit indices that should be inverted in order to convert the state of grid qubits to \(\ket{1}^{\otimes n_{g_d}}\).
`inversion_function`	The `Callable[[List[DimensionalReflectionData]], List[bool]]` function that converts the input data into a list of booleans that determine whether the directional velocity qubits should be inverted, per dimensions.
`invert_velocity_in_dimension`	The `List[bool]` obtained by calling the `inversion_function` on the `data`, indicating whether the directional velocity qubits should be inverted, per dimensions.
`is_near_corner_point`	The `bool` indicating whether the point is a near-corner point (used in 2D reflection).

Parameters:

data (List[DimensionalReflectionData])
dims_inside (List[int])
dims_outside (List[int])
inversion_function (Callable[[List[DimensionalReflectionData]], List[bool]])

class qlbm.lattice.geometry.ReflectionWall(dim, lower_bounds, upper_bounds, reflection_data)[source]#

Encodes the information required to perform reflection on a wall.

Each wall is encoded as fixed over one dimensions and spanning one or two alignment dimensions. This in turn models which qubits are used for the comparator operations of the reflection operators. The information required for the alignment dimensions only consists of bounds, while the fixed dimension uses its DimensionalReflectionData representation.

Class attributes#
Attribute	Description
`lower_bounds`	The `List[int]` of lower bounds for each dimension.
`upper_bounds`	The `List[int]` of upper bounds for each dimension.
`data`	The `DimensionalReflectionData` of the fixed dimension.
`dim`	The `int` indicating the fixed dimension.
`alignment_dims`	The `List[int]` indicating the one or two alignment dimensions.
`bounceback_loose_bounds`	The `List[List[bool]]` indicating whether the comparators should span the dimensions using tight (i.e., \(<\)) or loose (i.e., \(\leq\)) bounds.

Parameters:

dim (int)
lower_bounds (List[int])
upper_bounds (List[int])
reflection_data (DimensionalReflectionData)

class qlbm.lattice.geometry.ReflectionResetEdge(walls_joining, dims_of_edge, bounds_disconnected_dim, dimension_outside)[source]#

Encodes the information required to perform reflection on an edge in 3D.

An edge is encoded as 2 fixed points as DimensionalReflectionData objects, and one spanning dimension. This classes processes the information encoded in the reflection data object into boolean valued attributes that determine whether the directional velocity qubits should be inverted to perform reflection.

Class attributes#
Attribute	Description
`walls_joining`	The `List[DimensionalReflectionData]` containing the point data for the two fixed dimensions, stored in ascending order (\(x < y < z\)).
`dims_of_edge`	The `Tuple[int, int]` indicating the fixed dimensions.
`dim_disconnected`	The `int` indicating the dimension the edge spans.
`bounds_disconnected_dim`	The `Tuple[int, int]` that specifies the bounds of the edge in the dimension that it spans.
`reflected_velocities`	The `List[int]` that indicates to which dimensions the velocities that this edge affects belong to.
`invert_velocity_in_dimension`	The `List[bool]` indicating whether the directional velocity qubits should be inverted, per dimensions.
`is_corner_edge`	The `bool` indicating whether the edge is directly at the corner of the object.

Parameters:

walls_joining (List[DimensionalReflectionData])
dims_of_edge (Tuple[int, int])
bounds_disconnected_dim (Tuple[int, int])
dimension_outside (bool | None)

class qlbm.lattice.geometry.SpaceTimePWReflectionData(gridpoint_encoded, qubits_to_invert, velocity_indices_to_reflect, distance_from_boundary_point, lattice_properties)[source]#

Class encoding the necessary information for the reflection of a particle from asingle grid point in the STQBLM algorithm.

Attribute	Summary
`gridpoint_encoded`	The gridpoint encoded in the data.
`qubits_to_invert`	The grid qubit indices that have the value \(\ket{0}\).
`velocity_index_to_reflect`	The index of the qubit encoding the discrete velocity that should be reflected.
`distance_from_boundary_point`	The distance from the gridpoints where reflection takes place.
`lattice_properties`	The properties of the lattice in which reflection takes place.

Parameters:

gridpoint_encoded (Tuple[int, ...])
qubits_to_invert (List[int])
velocity_indices_to_reflect (List[int])
distance_from_boundary_point (Tuple[int, ...])
lattice_properties (SpaceTimeLatticeBuilder)

class qlbm.lattice.geometry.SpaceTimeVolumetricReflectionData(fixed_dim, ranged_dims, range_dimension_bounds, fixed_dimension_qubits_to_invert, fixed_gridpoint, velocity_index_to_reflect, distance_from_boundary_wall, lattice_properties)[source]#

Class encoding the necessary information for the reflection of a volumetric split of particles in the STQBLM algorithm.

Attribute	Summary
`fixed_dim`	The physical dimension that the volume does not span.
`ranged_dims`	The physical dimension(s) that the volume does span.
`range_dimension_bounds`	The bounds of the volume in each ranged dimension.
`fixed_dimension_qubits_to_invert`	The grid qubit indices that have the value \(\ket{0}\) for the fixed dimension.
`fixed_gridpoint`	The numerical value of the fixed gridpoint. Used for debugging purposes.
`velocity_index_to_reflect`	The index of the qubit encoding the discrete velocity that should be reflected.
`distance_from_boundary_wall`	The distance from the gridpoints where reflection takes place.
`lattice_properties`	The properties of the lattice in which reflection takes place.

Parameters:

fixed_dim (int)
ranged_dims (List[int])
range_dimension_bounds (List[Tuple[int, int]])
fixed_dimension_qubits_to_invert (List[int])
fixed_gridpoint (int)
velocity_index_to_reflect (int)
distance_from_boundary_wall (Tuple[int, ...])
lattice_properties (SpaceTimeLatticeBuilder)

class qlbm.lattice.geometry.SpaceTimeDiagonalReflectionData(bounds, step, distance_from_boundary_wall, lattice_properties)[source]#

Class encoding the necessary information for the reflection of a volumetric split of particles in the STQBLM algorithm.

Attribute	Summary
`fixed_dim`	The physical dimension that the volume does not span.
`ranged_dims`	The physical dimension(s) that the volume does span.
`range_dimension_bounds`	The bounds of the volume in each ranged dimension.
`fixed_dimension_qubits_to_invert`	The grid qubit indices that have the value \(\ket{0}\) for the fixed dimension.
`fixed_gridpoint`	The numerical value of the fixed gridpoint. Used for debugging purposes.
`velocity_index_to_reflect`	The index of the qubit encoding the discrete velocity that should be reflected.
`distance_from_boundary_wall`	The distance from the gridpoints where reflection takes place.
`lattice_properties`	The properties of the lattice in which reflection takes place.

Parameters:

bounds (List[Tuple[int, int]])
step (Tuple[int, ...])
distance_from_boundary_wall (Tuple[int, ...])
lattice_properties (SpaceTimeLatticeBuilder)

Lattices and Geometry#

Lattices#

Adaptable Lattice Register#

Geometry#

This Page